Математичні задачі тисячоліття
Протягом століть найкращі уми людства вирішували одну математичну задачу за іншою, проте є кілька, які досі не піддалися нікому. За знаходження алгоритму їх вирішення деякі фонди та компанії готові заплатити великі гроші.
1. Рівність класів P та NP
Якщо позитивну відповідь на якесь питання можна швидко (за поліноміальний час) перевірити (використовуючи деяку допоміжну інформацію, яка називається сертифікатом), то чи вірно, що й саму відповідь (разом із сертифікатом) на це питання можна швидко знайти? Задачі другого типу відносяться до класу P, першого до класу NP. Проблема рівності цих класів одна із найважливіших проблем теорії алгоритмів.
2. Гіпотеза Ходжа
Важлива проблема алгебраїчної геометрії. Гіпотеза описує класи когомологій на комплексних проективних різноманіттях, що реалізуються алгебраїчними підрізноманіттями.
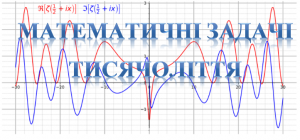
3. Гіпотеза Рімана
Гіпотеза свідчить, що всі нетривіальні (ті, що мають ненульову уявну частину) нулі дзета-функції Рімана мають дійсну частину 1/2. Її доказ чи спростування матиме далекосяжні наслідки для теорії чисел, особливо у сфері розподілу простих чисел..
4. Теорія Янга – Міллса
Задача в галузі фізики елементарних частинок. Потрібно довести, що для будь-якої простої компактної калібрувальної групи квантова теорія Янга — Міллса для чотиривимірного простору-часу існує і має ненульову спектральну щілину. Це твердження відповідає експериментальним даним та чисельному моделюванню, проте довести його досі не вдалося.
5. Існування та гладкість рішень рівнянь Навье – Стокса
Рівняння Навье – Стокса описують рух в’язкої рідини. Одне з найважливіших завдань гідродинаміки.
6. Гіпотеза Берча – Свіннертон-Дайєра
Гіпотеза пов’язана з рівняннями еліптичних кривих та множиною їх раціональних рішень.