День числа Ейлера
7 лютого вважають днем математичної константи e, яку також називають числом Ейлера або числом Непера.
Число e – фундаментальна математична константа. Це число є трансцендентним, тобто не може бути коренем якогось алгебраїчного рівняння з раціональними коефіцієнтами.
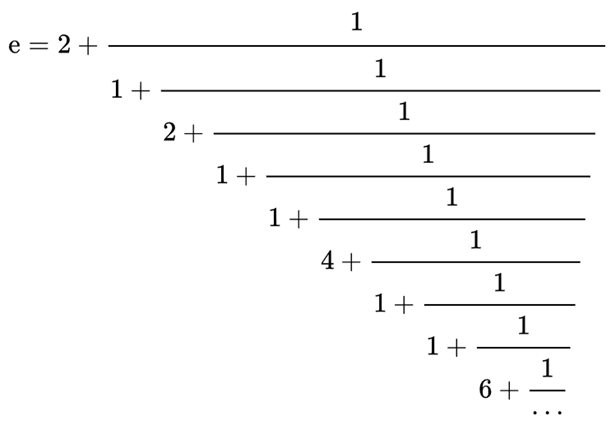
Перші 20 знаків числа e такі: e ≈ 2,71828182845904523536.
📝Відкрив цю константу швейцарський математик Якоб Бернуллі під час вивчення складних відсотків. У 1683 році Бернуллі досліджував, як швидко зростатимуть гроші, якщо їх нарощувати частіше ніж раз на рік. Припустимо, що хтось поклав 1$ у банк, який сплачує 4% річних на внесок. Якщо відсотки складні, то після кожного їх нарахування кількість грошей на рахунку збільшуватиметься і кожного наступного разу відсотки нараховуватимуться від збільшеної суми. Чим частіші нарахування, тим швидше збільшуватиметься вклад. Якщо нараховувати складні відсотки щороку, то 1$ за 25 років перетвориться у (1 + 0,04)25, тобто у 2,66$. Якщо нараховувати складні відсотки кожні півроку, то за 25 років долар перетвориться у (1 + 0,02)50, тобто у 2,69$.
Може скластися враження, що якщо нараховувати відсотки досить часто (наприклад, мільйон разів на рік), то за 25 років долар перетвориться у досить велику суму. Але насправді цього не відбудеться.
Через 25 років долар виросте до величини
(1 + 1/n)n,
де n — кількість нарахувань відсотків. Якщо необмежено збільшувати n, цей вираз прямуватиме до границі, яка дорівнює 2,718…, що лише на 3 центи більше за ту суму, яку б ми отримали, якщо б відсотки нараховувались один раз кожні півроку. Ця границя і називається числом e.
Понад 100 років потому Леонард Ейлер почав працювати з цією математичною константою, використовуючи позначення «e» від слова «експоненціальний».
Число е відіграє важливу роль у диференціальному й інтегральному численні, а також у багатьох застосуваннях математики, насамперед там, де йдеться про процеси експоненціального зростання. За таким законом тривають процеси:
🔸 зростання числа популяції – кількість представників популяції зростає експоненціально доти, доки є умови цього зростання (місце та їжа);
🔸 радіоактивного розпаду – прикладом є залежність енергії активації та швидкості хімічної реакції;
🔸зарядки і розрядки конденсатора.

